Motivation
In my Bitcoin PoW, Evolution of Trust article, I mentioned an interactive online (free-to-play) game called “The Evolution of Trust”.
Inspired by Robert Axelrod's 1984 book, The Evolution of Cooperation, Nicky Case, the designer of the game, explains how trust can be established in real life, based on the mathematical principles of game theory, in an interactive way with very pragmatic and entertaining interfaces.
Although the game contains mathematical game theory principles, Nicky's method of narration with funny characters is depicted with inspiring philosophical statements about life. I sincerely recommend that you play this game and even play it with your children.
In this article, I will try to explain how Bitcoin promises a revolutionary economy by simplifying the game theory narratives of “The Evolution of Trust” game and then by matching them through the characters of The Good, The Bad, and The Ugly movie.
Thus, emerging as an open, inclusive, and decentralized new finance, I'll emphasize why we should consider being “homo economicus”, which is the basic assumption of classical and neo-classical economics and means individuals who act rationally to maximize economic welfare.
The Good, The Bad, and The Ugly – A Game Theory Analysis
To find ground for the game theory principles in the Bitcoin economical trust revolution, I would like to refer to the characters and events of the 1966 Italian Spaghetti Western movie The Good, the Bad and the Ugly, starring Clint Eastwood, Lee Van Cleef, and Eli Wallach, which I think you've all watched.
As you know, the movie plots in events of Tuco (Ellie Walach), Angel Eyes/Sentenza (Lee Van Cliff), and Blondie (Clint Eastwood) competing remorselessly for a treasure left by Confederate troops.
All three duelers have a history together. They know that of the three, Angel Eyes is the most ruthless and no one benefits from allying with him. On the other hand, Blondie and Tuco have a history of lucrative cooperation.
The final scene in the movie might be the most outstanding example that fit the Bitcoin economical trust revolution. Let’s remember the final duel scene of the movie.
Let me briefly recall the stories behind the conflicts of interest between them.
Tuco (The Ugly) is an outlaw with a bounty on him. They travel around towns in collaboration with the cowboy named sniper Blondie (Good). Meanwhile, Sentenza, nicknamed Angel Eyes (The Bad), is on the trail of an ex-soldier who has seized a large amount of gold.
Just when Tuco is about to kill Blondie from thirst in the desert, their encounter with an ex-soldier, who is trailed by Sentenza, changes all plans. The soldier hid the gold in the cemetery on a front where the American Civil War was active. However, Tuco was able to learn the location of the cemetery and Blondie was able to learn the name of the grave.
The duo, who are forced to cooperate again, set out to search for the gold.
Tuco and Blondie, advancing at the front in their Southern uniforms, are captured by the Northerners. Sentenza is the Northern sergeant of the prison camp with his men. Sentenza tortures Tuco and learns where the gold is. When Sentenza realizes that Blondie knows which tomb the gold is buried in, they cooperate and move to the area where the graveyard is.
Meanwhile, Tuco escapes the Northern soldiers by jumping off the train. He finds Blondie and Sentenza. Tuco and Blonde team up again and kill Sentenza's men. Sentenza escapes. When they are close to reaching the gold; Tuco tricks Blondie and runs away but can't get rid of Blondie. Meanwhile, Sentenza is on its way to the graveyard. The trio meets in the graveyard, but only Blondie knows the name of the grave.
A three-way duel in the middle of the graveyard will determine the winner in a fight where dominance is constantly changing hands. The blonde writes the grave's name on the stone and challenges everyone to a duel. Blondie has supposedly put a message on a rock that holds the key to everything, but do the other two trusts Blondie to have actually written the correct answer?
It is better to team up with someone against the third dueler, rather than just draw and shoot at random. We need, however, to introduce another condition: because all three protagonists dealt with each other before, they have preferences over their respective ‘partner’.
Blondie, Angel Eyes, and Tuco have very strong desires especially when it comes to money.
As the other two evaluate the situation, they realize they can’t trust Blondie to have written the answer on the rock — therefore they can’t shoot Blondie who likely still has the answer.
Neither would fire at Blondie.
What they don’t know is that Blondie has given one an unloaded gun to Tuco!
Blondie has to worry about Sentenza who has the loaded gun will try to kill Tuco, the one with the unloaded gun. So, Blondie will fire at the one with the loaded gun, Sentenza.
As the camera passes from one face to the other the audience is meant to figure out what each would do.
In the final, Blondie shoots the guy with the loaded gun, Sentenza.
Game over!
Sentenza is known to be ruthless and has every incentive to keep it that way. It is thus a stable equilibrium. Because of that fact, and even though pay-offs are the same when teaming-up occurs, both Blondie and Tuco have incentives to cooperate and shoot Sentenza, which eventually happened.
In essence, there was little wise rationality, especially for Tuco. He is the distinguished second choice of both duelers, and he is better off with Blondie rather than Sentenza -per his own choices.
Remember, I highlighted in my article that “rational actors should define the game — not the game defines them.”
So, in the movie, this game was defined before it started.

Matching with The Evolution of Game Characters
Let's try to match the characters in the movie with the character definitions in Nicky Case's “The Evolution of Trust” game to simplify and clarify the win-win strategies with simple mathematical principles.
COPYCAT: Clint Eastwood as “Blondie”: The Good, a taciturn, confident bounty hunter, teams up with Tuco, and Angel Eyes temporarily, to find the buried gold. Blondie and Tuco have an ambivalent partnership.
ALWAYS COOPERATE: Eli Wallach as “Tuco”: The Ugly, a fast-talking, comically oafish yet also cunning, cagey, resilient, and resourceful Mexican bandit, is wanted by the authorities for a long list of crimes.
ALWAYS CHEAT: Lee Van Cleef as “Angel Eyes”: The Bad, a ruthless, confident, borderline-sadistic mercenary, takes pleasure in killing and always finishes a job for which he is paid, usually tracking and assassination.
As I mentioned in my previous Bitcoin Proof of Work (PoW), Evolution of Trust article, you want to build a distributed system like Bitcoin Blockchain on a scale-free network such as the internet. Anyone can participate in this system. You want the system to be self-organized and sustainable in a decentralized way with predetermined network protocols and rules. Finally, the system generates a value, in which the transfer (exchange) and the transform (payment) are placed between the participants.
Of course, since participation in the system is permissionless and there is a value proposition within the system, this value (the buried gold in the movie); some will try to get maximum income with a stupid effort as Tuco, some with bullying as Angel Eyes, and some with constantly following the most rational strategies under the current circumstances as Blondie.
Now while there are participants of this different character, and with no central authority (police, law, etc.) against cheaters or bullies, how do you ensure that this value remains hidden providing self-sovereignty to the participants in an egalitarian and decentralized way?
To simplify the topic and for a better understanding, let's develop simple mathematical principles on the basis of game theory.
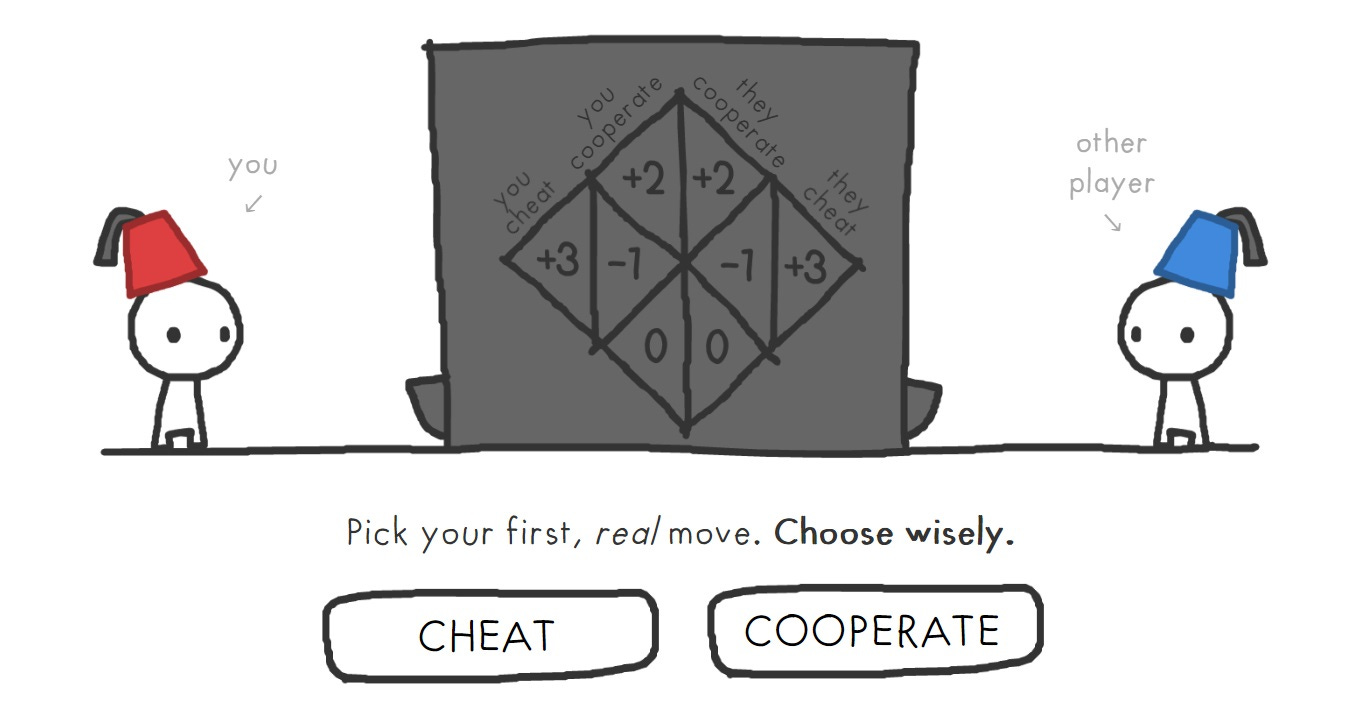
As game designer Nicky Case depicts in the Trust Game interface as shown in the figure below; there is a machine in the middle, and you throw mutual coins. The scoring shall be as given in the matrix table.
Here are the rules: If you and the other person cooperate, you both get +2 points. If you become a cheater and the other person becomes a cooperator, you gain +3 points, and the opponent loses -1 points or vice versa. If you both become cheaters, no one earns points.
Of course, the price (score) of being a cooperator or a cheater shall vary depending on the character of the other party.
For example, if your opponent is a rational (copycat) character, she/he shall act according to your moves. So, if you're a cooperator, she/he'll be a cooperator too. If you're a cheater, she/he'll be a cheater too (like the Blondie).
If the other person is the cooperator, she/he shall always be a cooperator (like the cheeky Tuco) whether you are a cooperator or a cheater. On the contrary, if the other person is a cheater, she/he shall always be a cheater whether you are a cooperator or a cheater (like Angel Eyes/ Sentenza).
At this point, please return to “The Evolution of Trust” game and click the “2. Repeated Game” section, look at the scores you get for always being a cheater or a cooperator with different characters.
Let's put these characters in place to better understand how the Bitcoin consensus mechanism works.
Let's start with the 3 actors I mentioned in my Bitcoin Proof of Work (PoW), Evolution of Trust article; (1) altruistic (always cooperator—pinkish), (2) rational (copycat—blue hats), and (3) malicious (always cheater—gray hats)
Let's simulate these character behaviors in a tournament according to the rules defined in the figure below. Points as depicted in the matrix table will be taken against the moves in each round. At the end of a certain number of rounds in the tournament, the winners (highest scorers) will be revealed.
Now according to the rules of this tournament, at the beginning of the system, there should only be 1 copycat (Blondie) and 1 always cheater (Angel Eyes), and the rest should always cooperator (Tuco). The tournament will be played in 10 rounds.
From the point of the Bitcoin Blockchain consensus mechanism; think of it as 1 miner (rational) who always wants to maximize his income in the system, 1 Byzantine (always cheater) who wants to take over the system for his own benefit, and all the remaining participants as node owners (always cooperator) who strictly follow predetermined protocols.
Now according to this simple real-life scenario supplemented with scientific strategies of game theory.
In your opinion who would win?
According to the rules we have set, in order to interactively see the points received in each round, those eliminated accordingly, and those who multiply (strengthen), please click on the “The Evolution of Trust” game's “5. The Evolution of Distrust" section.
When you do interactive experiments, you will see that at the end of the 10th round, the winners will always be the (increasingly multiplying) rationalists (copycats – blue hats)
But we have a problem here!
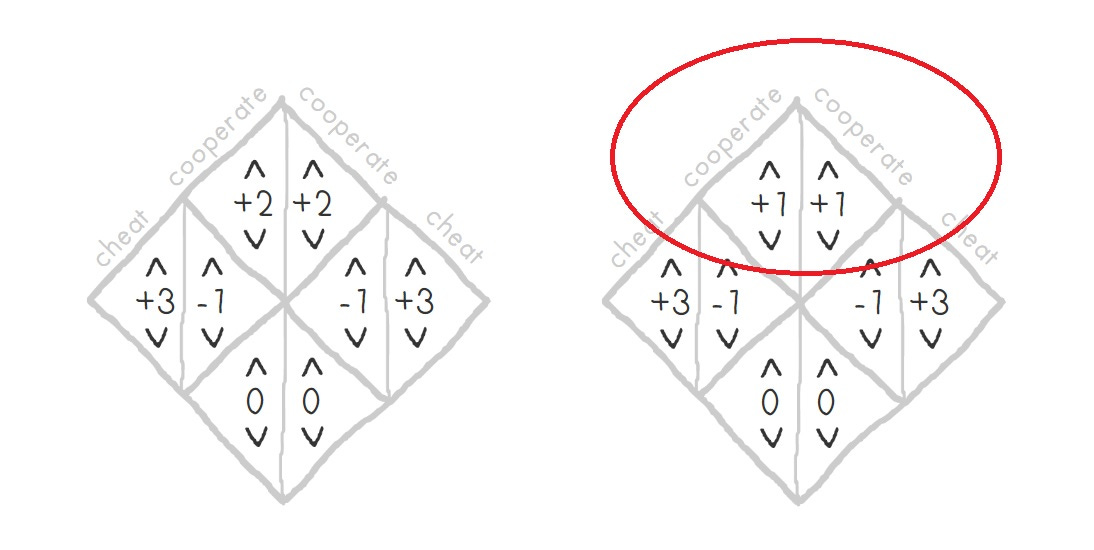
(1) If you reduce the number of tournament rounds to 5 or less, this time the winner will always be the -increasingly self-replicating- Byzantines (always cheaters).
(2) Besides, although the winners are rationalists (copycats) in any case when you reduce the +2 reward point to +1 point, the winners would be the Byzantines (always cheaters), again.
So why?
Reasons: (1) You need timing to bring your system to an adequate level of security. You also need time to build trust in real life. (2) If you want to create an incentive system focused on acting honestly, you need to set your incentives (rewards) correctly and determine an optimum value in each development (deflationary growth) process.
In the Bitcoin Blockchain system, (1) the block release state transition is set to 10 minutes (timing), and (2) the verified state history in the Bitcoin Blockchain data structure, that is, a certain number of Bitcoin correlations produced by cumulative computing power halving corresponds to the reward system (incentive).
Bitcoin halving system; Initially (2008), the 50 Bitcoin crypto money incentive reward given to each block production is halved approximately every 4 years (every 210,000 blocks — if each block production is approximately 10 minutes, it is approximately 3.99 years). Currently, (2022) block incentive reward is 6.25 BTC in Bitcoin Blockchain, which has applied 3 halving (2012, 2016, 2020) to date. The 4th halving will be in 2024, and the incentive to produce verified blocks will drop to 3,125 Bitcoin cryptocurrencies (50%). For miners, it can be understood as a relative incentive reward reduction. However, the limited supply of Bitcoin, set at 21 million units, is considered a high-income investment from the point of view of miners, as it provides both inflation resistance and the expectation that the value of Bitcoin will rise with the increase in Bitcoin circulation over time.
Of course, there are mechanisms in the Bitcoin Blockchain that support these two issues and are related to each other, but I'm trying to simplify it quite a lot. Please check out this article for some details.
Well, if there are only rationalists (copycats) in the system who respond with the same move to whatever the other person does, would this provide us with a secure system forever?
That would be against the theory of evolution or the 2nd law of thermodynamics (entropy)!
In other words, systems tend to a state of disorder, randomness, or uncertainty (entropy) in order for continuous renewal or evolution to occur. In simpler terms, in order for the next new one to be in the process of sustainable evolution, the previous old one should no longer work (after a while).
Therefore, it is inevitable that there be failures or errors in the systems. Since, any the slightest mistake, the rationalists respond to every move of the other with the same move, so they enter a pit of revenge, like Blondie and Tuco in the first scenes, and the system eventually collapses.
In the Bitcoin Blockchain, although some nodes have failures or behave maliciously, to be running at least 2/3 of the (honest) nodes become resistant to Byzantine fault tolerance, which means a threshold range in which the system can continue to work.
In other words, to be running at least 2/3 of the nodes in the system, we can assume that the system provides self-security and sustainability by constantly renewing itself, as an ideal disorder or entropy level state.
TAKEAWAYS
With the Bitcoin Blockchain, we try to figure out the potential of a new open, agentless, self-sovereign financial system. Bitcoin architecture was started with core algorithms. And with its game theory competitive-cooperative (co-opetition) strategies, the system has managed to keep itself the liveness and the safety for 13 years (2022).
Since the Bitcoin system is open to everyone, you do not need to perform controls such as authorization and authentication by an authority as in traditional central systems. Bitcoin Blockchain’s liveness and safety are again in an autonomous (self-organized) structure provided by the system participants.
In terms of system security, there is no concern that all of these actors should always be of a cooperative or rational character. With optimal incentive rewards and timing mechanisms applied, participants prefer to be rational (for profit maximization) and become a security shield that gets stronger each time with their verified transactions.
As I explained in this article, though most economists do not accept that humans can be rational economic people (homo economicus) for the benefit of society, the establishment of co-opetition (competitive and cooperation) based on the evolution of trust on the individual scale can allow the redefinition of financial markets as open, inclusive and decentralized.